During last night’s physics lecture, the professor discussed black-body radiation in the context of quantum mechanics. In physics, a black body is an idealized object that absorbs all electromagnetic radiation that hits it. Furthermore, if a black body exists at a constant temperature, then the radiation it emits is dependent on that temperature alone and no other characteristics.
According to classical physics, at smaller and smaller wavelengths of light, more and more radiation should be emitted from a black body. But it turns out this isn’t the case, and that at smaller wavelengths, the electromagnetic intensity drops off sharply. This discrepancy, called the ultraviolet catastrophe (because UV light is a short wavelength), remained a mystery for some time, until Planck came along and fixed things by introducing his eponymous constant.
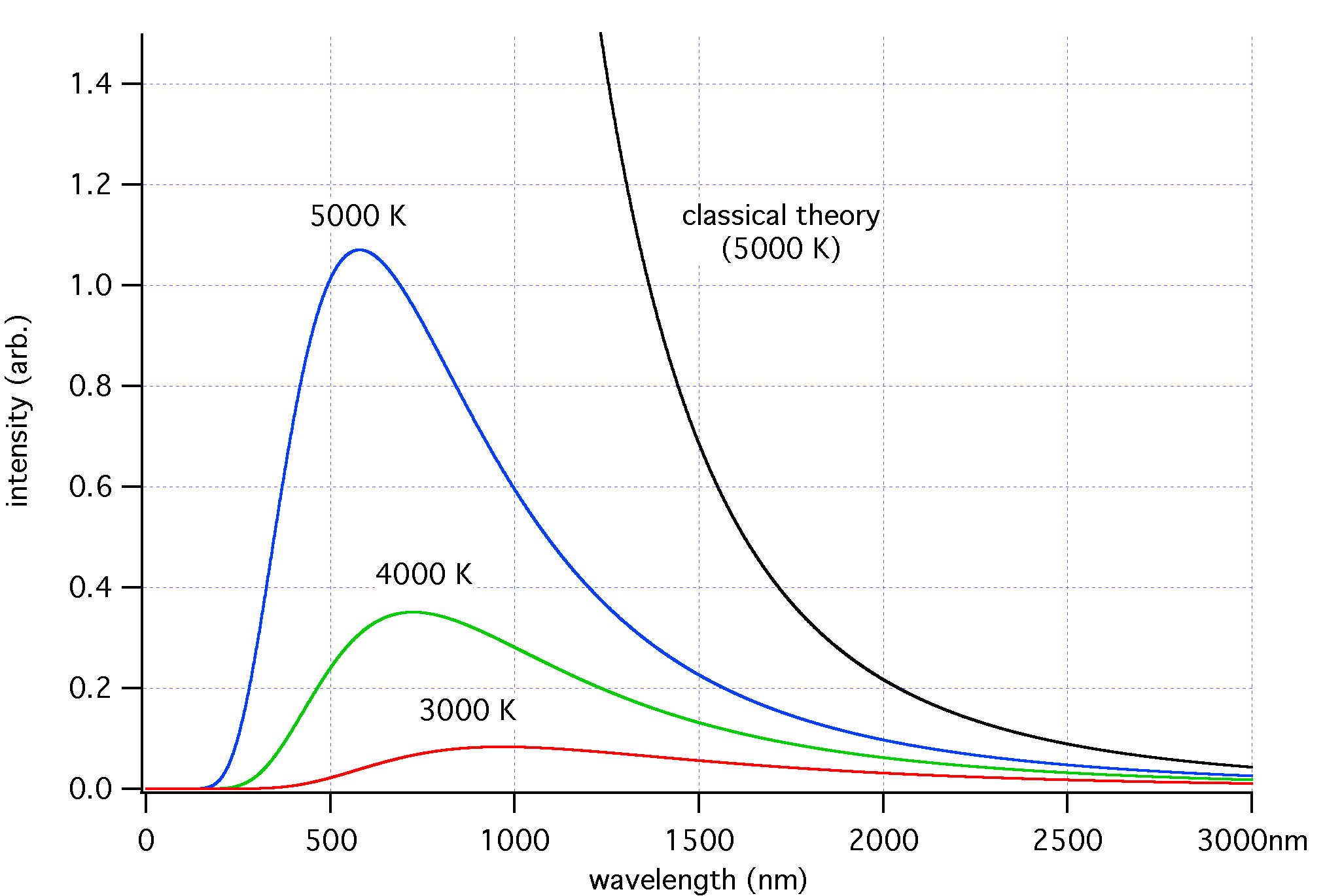 |
| Thanks, Wikipedia. |
The fix was to say that light is only emitted in discrete, quantized chunks with energy proportional to frequency. Explaining why this works is a little tricky, but the gist is that there are fewer electrons at higher energies, which means fewer photons get released, which means a lower intensity than predicted by classical electromagnetism. Planck didn’t know most of those details, but his correction worked anyway and kind of began the quantum revolution.
But all of that is beside the point. If black bodies are idealized, then you may be wondering how predictions about black bodies came to be so different form the observational data. How do you observe an idealized object? It turns out that the Sun is a near perfect real-world analog of a black body, and by studying its electromagnetic radiation scientists were able to study black-body radiation.
Anywho, my professor drew some diagrams of the Sun up on the board during this discussion and then proposed to us the following question: Can you use the equations for black-body radiation to predict the distance from the Earth to the Sun? As it turns out, the answer is yes.
You see, a consequence of Planck’s law is the Stefan-Boltzmann law, which says that the intensity of light emitted by a black body is proportional to the 4th power of the object’s temperature. That is, if you know the temperature of a black body, you know how energetic it is. How does that help us?
Well, the Sun emits a relatively static amount of light across its surface. A small fraction of that light eventually hits the Earth. What fraction of light hits the Earth is related to the how far away the Earth is from the Sun. The farther away the Sun is, the less light reaches the Earth. This is pretty obvious. It’s why Mercury is so hot and Pluto so cold. (But it’s not why summer is hot or winter cold.) So if we know the temperature of the Sun and the temperature of the Earth, we should be able to figure out how far one is from the other.
To do so, we have to construct a ratio. That is, we have to figure out what fraction of the Sun’s energy reaches the Earth. The Sun emits a sphere of energy that expands radially outward at the speed of light. By the time this sphere reaches the Earth, it’s very big. Now, a circle with the diameter of the Earth intercepts this energy, and the rest passes us by. So the fraction of energy we get is the area of the Earth’s disc divided by the surface area of the Sun’s sphere of radiation at the point that it hits the Earth. Here’s a picture:
 |
| I made this! |
So our ratio is this: Pe/Ps = Ae/As, where P is the power (energy per second) emitted by the body, Ae is the area of the Earth’s disc, and As is the surface area of the Sun’s energy when it reaches the Earth. One piece we’re missing from this is the Earth’s power. But we can get that just by approximating the Earth as a blackbody, too. This is less true than it is for the Sun, but it will serve our purposes nonetheless.
Okay, all we need now is the Stefan-Boltzmann law, which is I = σT4, where σ is a constant of proportionality that doesn’t actually matter here. What matters is that I, intensity, is power/area, and we’re looking for power. That means intensity times area equals power. So our ratio looks like this:
σTe44πre2 / σTs44πrs2 = πre2 / 4πd2
This is messy, but if you look closely, you’ll notice that a lot of those terms cancel out. When they do, we’re left with:
Te4 / Ts4rs2 = 1 / 4d2
Finally, d is out target variable. Solving for it, we get:
d = rsTs2 / 2Te2
Those variables are the radius of the Sun, the temperatures of the Sun and the Earth, and the number 2 (not a variable). Some googling tells me that the Sun’s surface temperature is 5778 K, the Earth’s surface temperature is 288 K, and the Sun’s radius is 696,342 km. If we plug those numbers into the above equation, out spits the answer: 1.40x1011 meters. As some of you may remember, the actual mean distance from the Earth to the Sun is 1.496x1011 meters, giving us an error of just 6.32%.
I’d say that’s pretty damn close. Why an error of 6%? Well, we approximated the Earth as a black body, but it’s actually warmer than it would be if it were a black body. So the average surface temperature we used is too high, thus making our answer too low. (There are other sources of error, too, but that’s probably the biggest one.)
There is one caveat to all this, however, which is that the calculation depends on the radius of the Sun. If you read the link above (which I recommend), you know, however, that we calculate the radius of the Sun based on the distance from the Earth to the Sun. But you can imagine that we know the radius of the Sun (to far less exact measurements) based solely on its observational characteristics. And in that case, we can still make the calculation.
Anywho, there’s your magic trick (physics problem) for the day. Enjoy.
No comments:
Post a Comment