I’m pretty sure I’ve talked a lot more about my math class than my physics class this semester. With the semester winding to a close, I don’t have much time life to even the score. But here’s an attempt. The reason for the relative silence on the subject of physics is, however, math-related.
As I mentioned in an earlier post, the third semester of intro physics is usually referred to as modern physics. At my community college, it’s “Waves, Optics, and Modern Physics.” The course covers a lot of disparate material. While the first half of the semester was pretty much all optics, the second half has been the modern physics component.
What does “modern physics” mean? Well, looking at the syllabus, it means a 7-week span in which we talked about relativity, quantum mechanics, atomic physics, and nuclear physics. All of these are entire fields unto themselves, but we spent no more than a week or two on each topic.
I predicted during the summer that I wouldn’t mind the abbreviated nature of the course, but that prediction turned out to be wrong. Here’s why.
The first two semesters of physics at my community college were, while not perfect by any stretch of the imagination, revelatory in comparison to the third semester. I enjoyed them a great deal because physical insight arose from mathematical foundations. With calculus, much of introductory physics becomes clear.
You can sit down and derive the equations of kinematics that govern how objects move in space. You can write integrals that tell you how charges behave next to particular surfaces. Rather than being told to plug and chug through a series of equations, you’re asked to use your knowledge of calculus to come up with ways to solve problems.
This is in stark contrast to what I remember of high school physics. There, we were given formulas plucked from textbooks and told to use them in a variety of word problems. Kinetic energy was 1/2mv2, because science. There was no physical insight to be gained, because there was no deeper understanding of the math behind the physics.
And so it is in modern physics as well. The mantra of my physics textbook has become, “We won’t go into the details.” Where before the textbook might say, “We leave the details as an exercise for the reader,” now there is no expectation that we could possibly comprehend the details. The math is “fairly complex,” we are told, but here are some formulas we can use in carefully circumscribed problems.
It happened during the optics unit, too. Light, when acting as a wave, reflects and refracts and diffracts. Why? Well, if you use a principle with no physical basis, you can derive some of the behaviors that light exhibits. But why would you use such a principle? Because you can derive some of the behaviors that light exhibits, of course.
But it’s much worse in modern physics. The foundation of quantum mechanics is the Schrödinger equation, which is a partial differential equation that treats particles as waves. Solutions to this equation are functions called Ψ (psi). What is Ψ? Well, it’s a function that, with some inputs, produces a complex number. Complex numbers have no physical meaning, however. For example, what would it mean to be the square root of negative one meters away from someone? Exactly.
So to get something useful out of Ψ, you have to square it. Doing so gives you the probability of finding a particle in some particular place or state. Why? Because you can’t be the square root of negative one meters away from someone, that’s why. The textbook draws a parallel between Ψ and the photon picture of diffraction, in which the square of something also represents a probability, but gives us no mathematical reason to believe this. Our professor didn’t even try and was in fact quite flippant about the hand-waving nature of the whole operation.
If you stick a particle (like an electron) inside of a box (like an atom), quantum mechanics and the Schrödinger equation tell you that the electron can only exist at specific energy levels. How do we find those energy levels? (This is the essence of atomic physics and chemistry, by the way.) Well, it involves “solving a transcendental equation by numerical approximation.” Great, let’s get started! “We won’t go into the details,” the textbook continues. Oh, I see.
Later, the textbook talks about quantum tunneling, the strange phenomenon by which particles on one side of a barrier can suddenly appear on the other side. How does this work? Well, it turns out the math is “fairly involved.” Oh, I see.
This kind of treatment goes on for much of the text.
Modern physics treats us as if we are high school students again. Explanations are either entirely absent or sketchy at best. Math is handed down on high in the form of equations to be used when needed. Insight is nowhere to be found.
Unfortunately, there might not be a great solution to this frustrating conundrum. While the basics of kinematics and electromagnetism can be understood with a couple semesters of calculus, modern physics seems to require a stronger mathematical foundation. But you can’t very well tell students to get back to the physics after a couple more years of math. That’s a surefire way to lose your students’ interest.
So we’re left with a primer course, where our appetites are whetted to the extent that our rudimentary tools allow. My interest in physics has not been stimulated, however. I’m no less interested than I was before, but what’s really on my mind is the math. More than the physics, I want to know the math behind it. No, I’m not saying I want to be a mathematician now. I’m just saying that I can’t be a physicist without being a little bit a mathematician.
Observations on science, science fiction, and whatever else my strange little brain finds interesting.
Friday, November 22, 2013
Thursday, November 14, 2013
Complexification
This post may seem a little out there, but that might be the point.
Last week in differential
equations we learned about a process our textbook called complexification. (You
can go ahead and google that, but near as I can tell what you’ll find is only vaguely
related to what my textbook is talking about.) Complexification is a way to
take a differential equation that looks like it’s about sines and cosines and
instead make it about complex exponentials. What does that mean?
Well, I think most people
know a little bit about sine and cosine functions. At the very least, I think
most people know what a sine wave looks like.
| Shout out to Wikipedia. |
Such a wave is produced by a
function that looks something like f(x) = sin(x). Sine and cosine come from
relationships between triangles and circles, but they can be used to model periodic,
fluctuating motion. For example, the way in which alternating current goes back
and forth between positive and negative is sinusoidal.
On the other hand,
exponential functions don’t seem at all related. Exponential functions look
something like f(x) = ex, and their graphs have shapes such as this:
| Thanks again, Wikipedia. |
Exponential functions are
used to model systems such as population growth or the spread of a disease.
These are systems where growth starts out small, but as the quantity being
measured grows larger, so too does the rate of growth.
Now, at first blush there
doesn’t appear to be a lot of common ground between sine functions and
exponential functions. But it turns out there is, if you throw in complex
numbers. What’s a complex number? It’s a number that includes i, the imaginary unit, which is defined
to be the square root of -1. You may have heard of this before, or you may have
only heard that you can’t take the square root of a negative number. Well, you
can: you just call it i.
So what’s the connection? The
connection is Euler’s formula, which looks like this:
eix = cos(x) + isin(x).
Explaining why this formula is true turns out to be very
complicated and a bit beyond what I can do. So just trust me on this one. (Or
look it up yourself and try to figure it out.) Regardless, by complexifying,
you have found a connection between exponentials and sinusoids.
How does that help with
differential equations? The answer is that complexifying your differential equation
can often make it simpler to solve.
Take the following differential
equation:
d2y/dt2
+ ky = cos(x).
This could be a model of an
undamped harmonic oscillator with a sinusoidal forcing function. It’s not
really important what that means, except to say you would guess (guessing
happens a lot in differential equations) that the solution to this equation
involves sinusoidal functions. The problem is, you don’t know if it will
involve sine, cosine, or some combination of the two. You can figure it out,
but it takes a lot of messy algebra.
A simpler way to do it is by
complexifying. You can guess instead that the solution will involve complex
exponentials, and you can justify this guess through Euler’s formula. After
all, there is a plain old cosine just sitting around in Euler’s formula,
implying that the solution to your equation could involve a term such as eix.
This idea of complexification
got me thinking about the topic of explaining things to people. You see, I
think I tend to do a bit of complexifying myself a lot of the time. Now, I don’t
mean I throw complex numbers into the mix when I don’t technically have to;
rather, I think I complexify by adding more than is necessary to my
explanations of things. I do this instead of simplifying.
Why would I do this? After
all, simplifying your explanation is going to make it easier for people to
understand. Complexifying, by comparison, should make things harder to understand.
But complexifying can also show connections that weren’t immediately obvious
beforehand. I mean, we just saw that complexifying shows a connection between
exponential functions and sinusoidal functions. Another example is
Euler’s identity, which can be arrived at by performing some algebra on Euler’s
formula. It looks like this:
eiπ + 1 = 0
This is considered by some to
be one of the most astounding equations in all of mathematics. It elegantly
connects five of the most important numbers we’ve discovered. Stare at it for
awhile and take it in. Can that identity really be true? Can those numbers
really be connected like that? Yup.
That, I think, is the benefit
of complexifying: letting us see what is not immediately obvious.
It turns out last week was
also Carl Sagan’s birthday. This generated some hubbub, with some praising the
man and others wishing we would just stop talking about him already. Carl Sagan
was admittedly before my time, but he has had an impact on me nonetheless. No,
he didn’t inspire me to study science or pick up the telescope or anything like
that. But I am rather fond of his pale blue dot speech, to the extent that there’s
even a minor plot point about it in one of my half-finished novels.
Now, I read some rather interesting
criticism of Sagan and his pale blue dot stuff on a blog I frequent. A
commenter was of the opinion that Sagan always made science seem grandiose and
inaccessible. That’s an interesting take, but I happen to disagree. Instead, I
think we might be able to conclude that Sagan engaged in a bit of
complexifying. No, he certainly didn’t make his material more difficult to
understand than it had to be; he was a very gifted communicator. What he did
do, however, and this is especially apparent with the pale blue dot, is make his
material seem very big, very out there. You might say he added more than was
necessary.
In doing so, he showed
connections that were not immediately obvious. The whole point of his pale blue
dot speech is that we are very small fish in a very big pond, and that this
connects us to each other. The distances and differences between people are,
relatively speaking, absolutely miniscule. From the outer reaches of the solar
system, all of humanity is just a pixel.
But there are more
connections to be made. Not only are all us connected to each other; we’re also
connected to the universe itself. Because, you see, from the outer reaches of
the solar system, we’re just a pixel next to other pixels, and those other
pixels are planets, stars, and interstellar gases. We’re all stardust, as has
been said.
This idea that seeing the world
as a tiny speck is transformative has been called by some (or maybe just Frank
White) the overview effect. Many astronauts have reported experiencing euphoria
and awe as a result of this effect. But going to space is expensive, especially
compared to listening to Carl Sagan.
So yeah, maybe Sagan was a
bit grandiose in the way he doled out his science. But I don’t think that’s a
bad thing. I just think it shows the connection between Sagan and my
differential equations class.
Wednesday, November 6, 2013
For My Next Trick...
I will calculate the distance from the Earth to the Sun using nothing but the Earth’s temperature, the Sun’s temperature, the radius of the Sun, and the number 2. How will I perform such an amazing feat of mathematical manipulation? Magic (physics), of course. And as a magician (physics student), I am forbidden from revealing the secrets of my craft (except on tests and this blog).
During last night’s physics lecture, the professor discussed black-body radiation in the context of quantum mechanics. In physics, a black body is an idealized object that absorbs all electromagnetic radiation that hits it. Furthermore, if a black body exists at a constant temperature, then the radiation it emits is dependent on that temperature alone and no other characteristics.
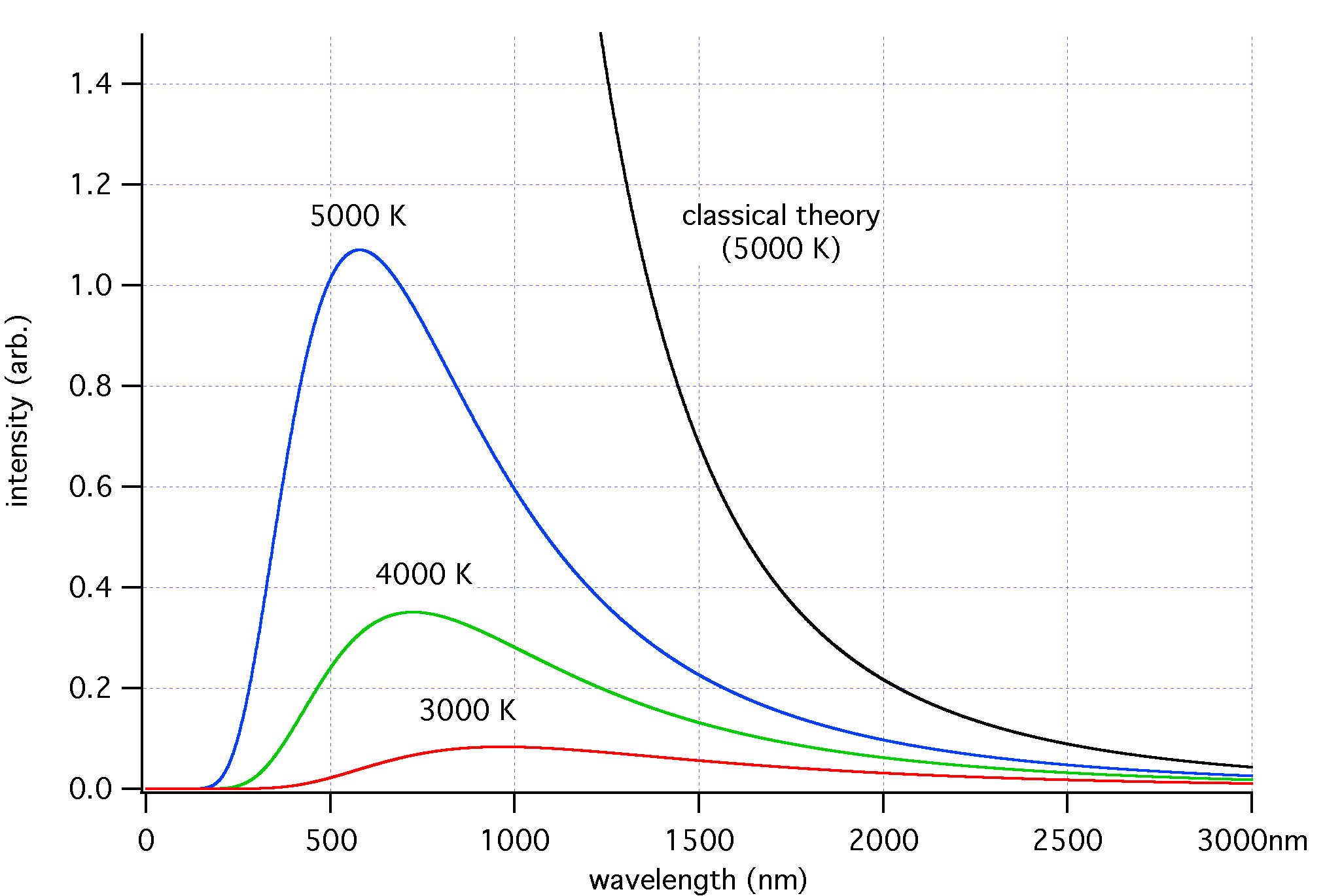
According to classical physics, at smaller and smaller wavelengths of light, more and more radiation should be emitted from a black body. But it turns out this isn’t the case, and that at smaller wavelengths, the electromagnetic intensity drops off sharply. This discrepancy, called the ultraviolet catastrophe (because UV light is a short wavelength), remained a mystery for some time, until Planck came along and fixed things by introducing his eponymous constant.
The fix was to say that light is only emitted in discrete, quantized chunks with energy proportional to frequency. Explaining why this works is a little tricky, but the gist is that there are fewer electrons at higher energies, which means fewer photons get released, which means a lower intensity than predicted by classical electromagnetism. Planck didn’t know most of those details, but his correction worked anyway and kind of began the quantum revolution.
But all of that is beside the point. If black bodies are idealized, then you may be wondering how predictions about black bodies came to be so different form the observational data. How do you observe an idealized object? It turns out that the Sun is a near perfect real-world analog of a black body, and by studying its electromagnetic radiation scientists were able to study black-body radiation.
Anywho, my professor drew some diagrams of the Sun up on the board during this discussion and then proposed to us the following question: Can you use the equations for black-body radiation to predict the distance from the Earth to the Sun? As it turns out, the answer is yes.
You see, a consequence of Planck’s law is the Stefan-Boltzmann law, which says that the intensity of light emitted by a black body is proportional to the 4th power of the object’s temperature. That is, if you know the temperature of a black body, you know how energetic it is. How does that help us?
Well, the Sun emits a relatively static amount of light across its surface. A small fraction of that light eventually hits the Earth. What fraction of light hits the Earth is related to the how far away the Earth is from the Sun. The farther away the Sun is, the less light reaches the Earth. This is pretty obvious. It’s why Mercury is so hot and Pluto so cold. (But it’s not why summer is hot or winter cold.) So if we know the temperature of the Sun and the temperature of the Earth, we should be able to figure out how far one is from the other.
To do so, we have to construct a ratio. That is, we have to figure out what fraction of the Sun’s energy reaches the Earth. The Sun emits a sphere of energy that expands radially outward at the speed of light. By the time this sphere reaches the Earth, it’s very big. Now, a circle with the diameter of the Earth intercepts this energy, and the rest passes us by. So the fraction of energy we get is the area of the Earth’s disc divided by the surface area of the Sun’s sphere of radiation at the point that it hits the Earth. Here’s a picture:
So our ratio is this: Pe/Ps = Ae/As, where P is the power (energy per second) emitted by the body, Ae is the area of the Earth’s disc, and As is the surface area of the Sun’s energy when it reaches the Earth. One piece we’re missing from this is the Earth’s power. But we can get that just by approximating the Earth as a blackbody, too. This is less true than it is for the Sun, but it will serve our purposes nonetheless.
Okay, all we need now is the Stefan-Boltzmann law, which is I = σT4, where σ is a constant of proportionality that doesn’t actually matter here. What matters is that I, intensity, is power/area, and we’re looking for power. That means intensity times area equals power. So our ratio looks like this:
σTe44πre2 / σTs44πrs2 = πre2 / 4πd2
This is messy, but if you look closely, you’ll notice that a lot of those terms cancel out. When they do, we’re left with:
Te4 / Ts4rs2 = 1 / 4d2
Finally, d is out target variable. Solving for it, we get:
d = rsTs2 / 2Te2
Those variables are the radius of the Sun, the temperatures of the Sun and the Earth, and the number 2 (not a variable). Some googling tells me that the Sun’s surface temperature is 5778 K, the Earth’s surface temperature is 288 K, and the Sun’s radius is 696,342 km. If we plug those numbers into the above equation, out spits the answer: 1.40x1011 meters. As some of you may remember, the actual mean distance from the Earth to the Sun is 1.496x1011 meters, giving us an error of just 6.32%.
I’d say that’s pretty damn close. Why an error of 6%? Well, we approximated the Earth as a black body, but it’s actually warmer than it would be if it were a black body. So the average surface temperature we used is too high, thus making our answer too low. (There are other sources of error, too, but that’s probably the biggest one.)
There is one caveat to all this, however, which is that the calculation depends on the radius of the Sun. If you read the link above (which I recommend), you know, however, that we calculate the radius of the Sun based on the distance from the Earth to the Sun. But you can imagine that we know the radius of the Sun (to far less exact measurements) based solely on its observational characteristics. And in that case, we can still make the calculation.
Anywho, there’s your magic trick (physics problem) for the day. Enjoy.
During last night’s physics lecture, the professor discussed black-body radiation in the context of quantum mechanics. In physics, a black body is an idealized object that absorbs all electromagnetic radiation that hits it. Furthermore, if a black body exists at a constant temperature, then the radiation it emits is dependent on that temperature alone and no other characteristics.
According to classical physics, at smaller and smaller wavelengths of light, more and more radiation should be emitted from a black body. But it turns out this isn’t the case, and that at smaller wavelengths, the electromagnetic intensity drops off sharply. This discrepancy, called the ultraviolet catastrophe (because UV light is a short wavelength), remained a mystery for some time, until Planck came along and fixed things by introducing his eponymous constant.
 |
| Thanks, Wikipedia. |
The fix was to say that light is only emitted in discrete, quantized chunks with energy proportional to frequency. Explaining why this works is a little tricky, but the gist is that there are fewer electrons at higher energies, which means fewer photons get released, which means a lower intensity than predicted by classical electromagnetism. Planck didn’t know most of those details, but his correction worked anyway and kind of began the quantum revolution.
But all of that is beside the point. If black bodies are idealized, then you may be wondering how predictions about black bodies came to be so different form the observational data. How do you observe an idealized object? It turns out that the Sun is a near perfect real-world analog of a black body, and by studying its electromagnetic radiation scientists were able to study black-body radiation.
Anywho, my professor drew some diagrams of the Sun up on the board during this discussion and then proposed to us the following question: Can you use the equations for black-body radiation to predict the distance from the Earth to the Sun? As it turns out, the answer is yes.
You see, a consequence of Planck’s law is the Stefan-Boltzmann law, which says that the intensity of light emitted by a black body is proportional to the 4th power of the object’s temperature. That is, if you know the temperature of a black body, you know how energetic it is. How does that help us?
Well, the Sun emits a relatively static amount of light across its surface. A small fraction of that light eventually hits the Earth. What fraction of light hits the Earth is related to the how far away the Earth is from the Sun. The farther away the Sun is, the less light reaches the Earth. This is pretty obvious. It’s why Mercury is so hot and Pluto so cold. (But it’s not why summer is hot or winter cold.) So if we know the temperature of the Sun and the temperature of the Earth, we should be able to figure out how far one is from the other.
To do so, we have to construct a ratio. That is, we have to figure out what fraction of the Sun’s energy reaches the Earth. The Sun emits a sphere of energy that expands radially outward at the speed of light. By the time this sphere reaches the Earth, it’s very big. Now, a circle with the diameter of the Earth intercepts this energy, and the rest passes us by. So the fraction of energy we get is the area of the Earth’s disc divided by the surface area of the Sun’s sphere of radiation at the point that it hits the Earth. Here’s a picture:
 |
| I made this! |
So our ratio is this: Pe/Ps = Ae/As, where P is the power (energy per second) emitted by the body, Ae is the area of the Earth’s disc, and As is the surface area of the Sun’s energy when it reaches the Earth. One piece we’re missing from this is the Earth’s power. But we can get that just by approximating the Earth as a blackbody, too. This is less true than it is for the Sun, but it will serve our purposes nonetheless.
Okay, all we need now is the Stefan-Boltzmann law, which is I = σT4, where σ is a constant of proportionality that doesn’t actually matter here. What matters is that I, intensity, is power/area, and we’re looking for power. That means intensity times area equals power. So our ratio looks like this:
σTe44πre2 / σTs44πrs2 = πre2 / 4πd2
This is messy, but if you look closely, you’ll notice that a lot of those terms cancel out. When they do, we’re left with:
Te4 / Ts4rs2 = 1 / 4d2
Finally, d is out target variable. Solving for it, we get:
d = rsTs2 / 2Te2
Those variables are the radius of the Sun, the temperatures of the Sun and the Earth, and the number 2 (not a variable). Some googling tells me that the Sun’s surface temperature is 5778 K, the Earth’s surface temperature is 288 K, and the Sun’s radius is 696,342 km. If we plug those numbers into the above equation, out spits the answer: 1.40x1011 meters. As some of you may remember, the actual mean distance from the Earth to the Sun is 1.496x1011 meters, giving us an error of just 6.32%.
I’d say that’s pretty damn close. Why an error of 6%? Well, we approximated the Earth as a black body, but it’s actually warmer than it would be if it were a black body. So the average surface temperature we used is too high, thus making our answer too low. (There are other sources of error, too, but that’s probably the biggest one.)
There is one caveat to all this, however, which is that the calculation depends on the radius of the Sun. If you read the link above (which I recommend), you know, however, that we calculate the radius of the Sun based on the distance from the Earth to the Sun. But you can imagine that we know the radius of the Sun (to far less exact measurements) based solely on its observational characteristics. And in that case, we can still make the calculation.
Anywho, there’s your magic trick (physics problem) for the day. Enjoy.
Friday, November 1, 2013
National Hard Things Take Practice Month
Okay, it doesn’t have quite the same ring to it as National Novel Writing Month, but I’m saving my good words for my, well, novel writing. As some of you may know, November is NaNoWriMo, a worldwide event during which a bunch of people get together to (individually) write 50,000 words in 30 days. I’ve done it the last several years and I’m doing it this year, too. It’s hard, it’s fun, and it’s valuable.
As some of you may also know, Laura Miller, a writer for Salon, published a piece decrying NaNoWriMo. (Turns out she published that piece 3 years ago, but it's making the rounds now because NaNo is upon us. Bah, I'm still posting.) This made a lot of wrimos pretty upset, and I’ve seen some rather vitriolic criticism in response. Miller’s main point seems to be that there’s already enough crap out there and we don’t need to saturate the world with more of it. Moreover, she thinks we could all do a little more reading and a little less writing.
Well, as a NaNoWriMo participant and self-important blogger, I think I’m going to respond to Miller’s criticism. Of course, maybe that’s exactly what she wants. By writing this now, I’m not writing my NaNo novel. Dastardly plan, Laura Miller.
Now, I understand the angry response to Miller’s piece. I really do. It has a very “get off my lawn” feel to it that seems to miss the point that, for a lot of people, NaNo is just plain fun. But her two points aren’t terrible points, and I think they’re worth responding to in a civil, constructive way. So here goes.
As is obvious to anyone who’s read this blog, I quite like science. That’s what the blog is about, after all. In fact, I’ve been interested in science ever since I was a child. I read books about science, I had toy science kits, and I loved science fiction as a genre.
Yet this blog about science is not even a year old, and I’m writing this post as a freshly minted 28 year old. Why is that? Because up until about 2 years, I didn’t do anything with my interest in science. I took plenty of science and math classes in high school, but I mostly dithered around in them and didn’t, you guessed it, practice.
It wasn’t until 2 years ago that I sat down and decided it was time to reteach myself calculus. And how did I teach myself calculus? By giving myself homework. By doing that homework. By checking my answers and redoing problems until I got them right. And now I can do calculus. Now I can do linear algebra, differential equations, and physics. I’m no expert in these subjects, but I understand them to a degree because I’ve done them. I’ve practiced, just like you practice a sport.
The analogy here should be clear. You have to practice your sport, you have to practice your math, you have to practice your writing. Where some may disagree with this analogy is the idea that writing 50,000 words worth of drivel counts as practice. The answer is that it’s practicing one skill of writing, but not all writing skills. This follows from the analogy, too. Sometimes you practice free throws; other times you practice taking integrals. Each is a specific skill within a broad field, and each takes practice.
And as any writer knows, sometimes the most difficult part of writing is staring at a blank white page and trying to find some way to put some black on it. We all have ideas. We all have stories and characters in our heads. But exorcising those thoughts onto paper is a skill wholly unto itself, apart from the skills of grammar, narrative, and prose.
So it needs practice, and NaNoWriMo is that practice. If you’re a dedicated writer, however, then it follows that NaNo should not be your only practice. You have to practice the other skills, too. You have to write during the rest of the year, and you have to pay attention to grammar, narrative, and prose. But taking one month to practice one skill hardly seems a waste.
I’ve less to say about Miller’s second point, that we should read more and write less. This is a matter of opinion, I suppose. But I do have one comment about it. America is often criticized as being a nation of consumers who voraciously eat up every product put before them. We are asked only to choose between different brand names and to give no more thought to our decisions than which product to purchase.
Writing is a break from that. Rather than being a lazy, passive consumer of other people’s ideas, writing forces you to formulate and express your own ideas. Writing can be a tool of discovery, a way to expand the thinking space we all inhabit. Rather than selecting an imperfect match from a limited set of options, writing lets you make a choice that is precisely what you want it to be. You get to declare where you stand, or that you’re not taking a stand at all. You get to have a voice beyond simply punching a hole in a ballot.
You shouldn’t write instead of read, but you should write (or find some other way to creatively express your identity).
As some of you may also know, Laura Miller, a writer for Salon, published a piece decrying NaNoWriMo. (Turns out she published that piece 3 years ago, but it's making the rounds now because NaNo is upon us. Bah, I'm still posting.) This made a lot of wrimos pretty upset, and I’ve seen some rather vitriolic criticism in response. Miller’s main point seems to be that there’s already enough crap out there and we don’t need to saturate the world with more of it. Moreover, she thinks we could all do a little more reading and a little less writing.
Well, as a NaNoWriMo participant and self-important blogger, I think I’m going to respond to Miller’s criticism. Of course, maybe that’s exactly what she wants. By writing this now, I’m not writing my NaNo novel. Dastardly plan, Laura Miller.
Now, I understand the angry response to Miller’s piece. I really do. It has a very “get off my lawn” feel to it that seems to miss the point that, for a lot of people, NaNo is just plain fun. But her two points aren’t terrible points, and I think they’re worth responding to in a civil, constructive way. So here goes.
As is obvious to anyone who’s read this blog, I quite like science. That’s what the blog is about, after all. In fact, I’ve been interested in science ever since I was a child. I read books about science, I had toy science kits, and I loved science fiction as a genre.
Yet this blog about science is not even a year old, and I’m writing this post as a freshly minted 28 year old. Why is that? Because up until about 2 years, I didn’t do anything with my interest in science. I took plenty of science and math classes in high school, but I mostly dithered around in them and didn’t, you guessed it, practice.
It wasn’t until 2 years ago that I sat down and decided it was time to reteach myself calculus. And how did I teach myself calculus? By giving myself homework. By doing that homework. By checking my answers and redoing problems until I got them right. And now I can do calculus. Now I can do linear algebra, differential equations, and physics. I’m no expert in these subjects, but I understand them to a degree because I’ve done them. I’ve practiced, just like you practice a sport.
The analogy here should be clear. You have to practice your sport, you have to practice your math, you have to practice your writing. Where some may disagree with this analogy is the idea that writing 50,000 words worth of drivel counts as practice. The answer is that it’s practicing one skill of writing, but not all writing skills. This follows from the analogy, too. Sometimes you practice free throws; other times you practice taking integrals. Each is a specific skill within a broad field, and each takes practice.
And as any writer knows, sometimes the most difficult part of writing is staring at a blank white page and trying to find some way to put some black on it. We all have ideas. We all have stories and characters in our heads. But exorcising those thoughts onto paper is a skill wholly unto itself, apart from the skills of grammar, narrative, and prose.
So it needs practice, and NaNoWriMo is that practice. If you’re a dedicated writer, however, then it follows that NaNo should not be your only practice. You have to practice the other skills, too. You have to write during the rest of the year, and you have to pay attention to grammar, narrative, and prose. But taking one month to practice one skill hardly seems a waste.
I’ve less to say about Miller’s second point, that we should read more and write less. This is a matter of opinion, I suppose. But I do have one comment about it. America is often criticized as being a nation of consumers who voraciously eat up every product put before them. We are asked only to choose between different brand names and to give no more thought to our decisions than which product to purchase.
Writing is a break from that. Rather than being a lazy, passive consumer of other people’s ideas, writing forces you to formulate and express your own ideas. Writing can be a tool of discovery, a way to expand the thinking space we all inhabit. Rather than selecting an imperfect match from a limited set of options, writing lets you make a choice that is precisely what you want it to be. You get to declare where you stand, or that you’re not taking a stand at all. You get to have a voice beyond simply punching a hole in a ballot.
You shouldn’t write instead of read, but you should write (or find some other way to creatively express your identity).
Wednesday, October 23, 2013
Tip o' the Lance
My weekend activities have provided me with ample blogging fodder of late. This past weekend I went to a local Renaissance Festival and, among other things, watched some real life jousting. That is, actual people got on actual horses and actually rammed lances into each other, sometimes with spectacular results.
At one point a lance tip broke off on someone’s armor and went flying about 50 feet into the air. A friend wondered aloud what kind of force it would take to achieve that result, and here I am to do the math. This involves some physics from last year as well as much more complicated physics that I can’t do. You see, if a horse glided along the ground without intrinsic motive power, and were spherical, and of uniform density… but alas, horses are not cows.
Anywho, as to the flying lance tip, the physics is pretty easy. Now, I can’t say what force was acting on the lance. The difficulty is that, from a physics standpoint, the impact between the lance and the armor imparted momentum into the lance tip. Newton’s second law (in differential form) tells us that force is equal to the change in momentum over time. Thus, in order to calculate the force of the impact, I have to know how long the impact took. I could say it was a split second or an instant, but I’m looking for a little more precision than that.
Instead, however, I can tell you how much energy the lance tip had. It takes a certain amount of kinetic energy to fly 50 feet into the air. We’re gonna say the lance tip weighs 1 kg (probably an overestimate) and that it climbed 15 meters before falling down. In that case, our formula is e = mgh, where g is 9.8 m/s2 of gravitational acceleration, and we’re at about 150 joules of energy. This is roughly as much energy as a rifle bullet just exiting the muzzle. It also means the lance tip had an initial speed of about 17 m/s. I’m ignoring here, because I don’t have enough data, that the lance tip spun through the air—adding rotational energy to the mix—and that there was a sharp crack from the lance breaking—adding energy from sound.
But this doesn’t conclude our analysis. For starters, where did the 150 joules of energy come from? And is that all the energy of the impact? Let’s answer the second question first. Another pretty spectacular result of the jousting we witnessed was that one rider was unhorsed. We can model being unhorsed as moving at a certain speed and then having your speed brought to 0. Some googling tells me that a good estimate for the galloping speed of a horse is 10 m/s.
So the question is, how much work does it take to unhorse a knight? With armor, a knight probably weighs 100 kg. Traveling at 10 m/s, our kinetic energy formula tells us this knight possesses 5000 joules of energy, which means the impact must deliver 5000 joules of energy to stop the knight. This means there’s certainly enough energy to send a lance tip flying, and it also means that not all of the energy goes into the lance tip.
We can apply the same kinetic energy formula to our two horses, which each weigh about 1000 kg, and see that there’s something like 100 kj of energy between the two. Not all of that goes into the impact, however, because both horses keep going. This is where the horses not being idealized points hurts the analysis. Were that so, we might be able to tell how much energy is “absorbed” by the armor and lance.
There is one final piece of data we can look at. I estimate the list was 50 meters long. The knights met at the middle and, if they timed things properly, reached their maximum speeds at that point. Let’s also say that horses are mathematically simple and accelerate at a constant rate. One of the 4 basic kinematic equations tells us that vf2 = vi2 + 2ad. So this is 100 = 0 + 2*a*25, and solving for a gets us an acceleration of 2 m/s2. Newton’s second law, f=ma, means each horse was applying 2000 newtons of force to accelerate at that rate. 2000 N across 25 meters is 50,000 joules of work. It takes 5 seconds to accelerate to 10 m/s at 2 m/s2, so 50,000 joules / 5 seconds = 10,000 watts of power. What’s 10,000 watts? Well, let’s convert that to a more recognizable unit of measure. 10 kW comes out to about 13 horsepower, which is about 13 times as much power as a horse is supposed to have. Methinks James Watt has some explaining to do.
One other thought occurred to me during this analysis. Some googling tells me there are roughly 60 million horses in the world. If a horse can pump out 10 kW of energy, then we have roughly 600 GW of energy available from horses alone. Wikipedia says our average power consumption is 15 TW, which means the world’s horses running on treadmills could provide 4% of the energy requirements of the modern world. This isn’t strictly speaking true, because there will be losses due to entropy (and you can’t run a horse nonstop), but it’s in the right ballpark. Moral of the story? Don’t let anyone tell you that energy is scarce. The problem isn’t that there isn’t enough energy in the world; it’s that we don’t have the industry and infrastructure necessary to use all the energy at our disposal.
 |
| I didn't take this picture. It's from the Renn Fest website. I just think my blog needs more visuals. |
Anywho, as to the flying lance tip, the physics is pretty easy. Now, I can’t say what force was acting on the lance. The difficulty is that, from a physics standpoint, the impact between the lance and the armor imparted momentum into the lance tip. Newton’s second law (in differential form) tells us that force is equal to the change in momentum over time. Thus, in order to calculate the force of the impact, I have to know how long the impact took. I could say it was a split second or an instant, but I’m looking for a little more precision than that.
Instead, however, I can tell you how much energy the lance tip had. It takes a certain amount of kinetic energy to fly 50 feet into the air. We’re gonna say the lance tip weighs 1 kg (probably an overestimate) and that it climbed 15 meters before falling down. In that case, our formula is e = mgh, where g is 9.8 m/s2 of gravitational acceleration, and we’re at about 150 joules of energy. This is roughly as much energy as a rifle bullet just exiting the muzzle. It also means the lance tip had an initial speed of about 17 m/s. I’m ignoring here, because I don’t have enough data, that the lance tip spun through the air—adding rotational energy to the mix—and that there was a sharp crack from the lance breaking—adding energy from sound.
But this doesn’t conclude our analysis. For starters, where did the 150 joules of energy come from? And is that all the energy of the impact? Let’s answer the second question first. Another pretty spectacular result of the jousting we witnessed was that one rider was unhorsed. We can model being unhorsed as moving at a certain speed and then having your speed brought to 0. Some googling tells me that a good estimate for the galloping speed of a horse is 10 m/s.
So the question is, how much work does it take to unhorse a knight? With armor, a knight probably weighs 100 kg. Traveling at 10 m/s, our kinetic energy formula tells us this knight possesses 5000 joules of energy, which means the impact must deliver 5000 joules of energy to stop the knight. This means there’s certainly enough energy to send a lance tip flying, and it also means that not all of the energy goes into the lance tip.
We can apply the same kinetic energy formula to our two horses, which each weigh about 1000 kg, and see that there’s something like 100 kj of energy between the two. Not all of that goes into the impact, however, because both horses keep going. This is where the horses not being idealized points hurts the analysis. Were that so, we might be able to tell how much energy is “absorbed” by the armor and lance.
There is one final piece of data we can look at. I estimate the list was 50 meters long. The knights met at the middle and, if they timed things properly, reached their maximum speeds at that point. Let’s also say that horses are mathematically simple and accelerate at a constant rate. One of the 4 basic kinematic equations tells us that vf2 = vi2 + 2ad. So this is 100 = 0 + 2*a*25, and solving for a gets us an acceleration of 2 m/s2. Newton’s second law, f=ma, means each horse was applying 2000 newtons of force to accelerate at that rate. 2000 N across 25 meters is 50,000 joules of work. It takes 5 seconds to accelerate to 10 m/s at 2 m/s2, so 50,000 joules / 5 seconds = 10,000 watts of power. What’s 10,000 watts? Well, let’s convert that to a more recognizable unit of measure. 10 kW comes out to about 13 horsepower, which is about 13 times as much power as a horse is supposed to have. Methinks James Watt has some explaining to do.
One other thought occurred to me during this analysis. Some googling tells me there are roughly 60 million horses in the world. If a horse can pump out 10 kW of energy, then we have roughly 600 GW of energy available from horses alone. Wikipedia says our average power consumption is 15 TW, which means the world’s horses running on treadmills could provide 4% of the energy requirements of the modern world. This isn’t strictly speaking true, because there will be losses due to entropy (and you can’t run a horse nonstop), but it’s in the right ballpark. Moral of the story? Don’t let anyone tell you that energy is scarce. The problem isn’t that there isn’t enough energy in the world; it’s that we don’t have the industry and infrastructure necessary to use all the energy at our disposal.
Friday, October 18, 2013
Salute Your Solution Space
Last weekend I went to an SF writing convention at which the esteemed George R. R. Martin himself was guest of honor. I had a good time, managed to snag an autograph, and even got conclusive proof that he is, in fact, working on The Winds of Winter. (He read 2 chapters.) So my blog post for today is inspired by the convention visit, but has nothing to do with science fiction, writing, or ASOIAF.
The most interesting panel at the convention, personally, wasn’t even a panel at all. It was a talk given by computer scientist Dr. Alice Armstrong on artificial intelligence and how to incorporate AI into stories without pissing off people like Dr. Alice Armstrong. It was an amusing and informative talk, although not as many people laughed at her jokes as should have. A couple points she made resonated particularly well with me, not because of my fiction, but because of my math courses the past two semesters.
Specifically, about a quarter of her talk was given over to the concept of genetic algorithms, in which a whole bunch of possible solutions to a problem are tested, mutated, combined, and tested again until a suitable solution is found. This is supposed to mirror the concept of biological evolution, however Dr. Armstrong pointed out numerous times that the similarities are, at this point, rather superficial.
But one thing she said is that genetic algorithms are essentially search engines. They go through an infinite landscape of possible solutions—the solution space—and come out with one that will work. This reminded me of a topic covered in linear algebra, and one we’re covering again from a different perspective in differential equations. The solution space in differential equations is a set of solutions arrived at by finding the eigenvectors of a system of linear differential equations.
Bluh, what? First, let’s talk about differential equations. Physics is rife with differential equations—equations that describe how systems change—because physics is all about motion. What kind of motion? Motion like, for example, a cat falling from up high. As we all know, cats tend to land on their feet. They start up high and maybe upside down, they twist around in the air, and by the time they reach the ground they’re feet down (unless buttered toast is involved).
If you could describe this mathematically, you’d need an equation that deals with lots of change, like, say, a differential equation. In fact, you might even need a system of differential equations, because you have to keep track of the cat’s shape, position, speed, and probably a few other variables.
Going back to linear algebra for a moment, you can perform some matrix operations on this system of differential equations to produce what are called eigenvectors. It’s not really important what eigenvectors are, except to know that they form the basis for the solution space.
To explain what a basis is, I’m going to steal from Dr. Armstrong for a moment. The example she gave of a genetic algorithm at work was one in which a “population” of cookie recipes are baked, and the more successful recipes pass on their “genes” to the next generation. A gene, in this sense, is the individual components of the recipe: sugar, flour, chocolate chips, etc.
You have some number of cups of sugar, add that onto some number of cups of flour, add that onto some number of cups of chocolate chips, and so on, and you have a cookie recipe. These linear combinations of ingredients—different numbers of cups—can be used to form a vast set of cookie recipes, a solution space of cookie recipes, if you will. So a basis is the core ingredients with which you can build an infinite variety of a particular item.
Let’s get back to our cat example. If you take a system of linear differential equations about falling cats and find their eigenvectors, then you will have a basis for the solution space of cat falling. That is, you will know an infinite number of ways that a cat can fall, given some initial conditions. But what ways of falling are better than others? That’s where genetic algorithms come in.
In our case, a genetic algorithm is what produced the cat righting reflex. You see, as we discovered, there are an infinite number of ways for a cat to fall. (While there are an infinite number of solutions, infinity is not everything. For example, there are an infinite number of numbers between 0 and 1, but the numbers between 0 and 1 are not all the numbers. Similarly, there are ways in which you can arrange the equations of cat falling that don’t produce meaningful results, like a cat falling up, so these aren’t a part of the infinite solution space.)
It would take a very long time to search through an infinite number of cat falling techniques to find the best one. Genetic algorithms, then, take a population of cats, have a lot of them fall, and see which ones fall better than others. This is, of course, natural selection. Now, you may think of evolution as a slow process, but it’s important to remember that this genetic algorithm is not just testing the fitness of cat falling, but of every other way in which a cat could possibly die. From that standpoint, evolution has done an absolutely remarkable job of creating an organism that can survive in a great many situations.
If you don’t believe me, consider that there is a Wikipedia page dedicated to the “falling cat problem” which, among other things, compares the mathematics of falling cats to the mathematics of quantum chromodynamics (which I don’t understand a lick of, btw).
Some of you may be wondering how what is essentially a search algorithm can be considered a form of “artificial intelligence.” Well, to answer that question, you have to give a good definition of what intelligence really is. But this blog post is probably long enough already, so I’m not going down that road. Consider for a moment, however, that there is a certain segment of the population that is absolutely convinced life originated via intelligent design. While their opinion on this matter is almost always bound up in belief, it’s not hard to look at nature and see something intelligent. If nothing else, nature produced humans, and it’s difficult to imagine any definition of intelligence that doesn’t include us (despite our occasional idiocy).
One final note: I lied in the beginning. I think Solution Space would make an excellent title for an SF story, so there’s your connection to science fiction and writing. And don’t steal my title, Mr. Martin.
The most interesting panel at the convention, personally, wasn’t even a panel at all. It was a talk given by computer scientist Dr. Alice Armstrong on artificial intelligence and how to incorporate AI into stories without pissing off people like Dr. Alice Armstrong. It was an amusing and informative talk, although not as many people laughed at her jokes as should have. A couple points she made resonated particularly well with me, not because of my fiction, but because of my math courses the past two semesters.
Specifically, about a quarter of her talk was given over to the concept of genetic algorithms, in which a whole bunch of possible solutions to a problem are tested, mutated, combined, and tested again until a suitable solution is found. This is supposed to mirror the concept of biological evolution, however Dr. Armstrong pointed out numerous times that the similarities are, at this point, rather superficial.
But one thing she said is that genetic algorithms are essentially search engines. They go through an infinite landscape of possible solutions—the solution space—and come out with one that will work. This reminded me of a topic covered in linear algebra, and one we’re covering again from a different perspective in differential equations. The solution space in differential equations is a set of solutions arrived at by finding the eigenvectors of a system of linear differential equations.
Bluh, what? First, let’s talk about differential equations. Physics is rife with differential equations—equations that describe how systems change—because physics is all about motion. What kind of motion? Motion like, for example, a cat falling from up high. As we all know, cats tend to land on their feet. They start up high and maybe upside down, they twist around in the air, and by the time they reach the ground they’re feet down (unless buttered toast is involved).
If you could describe this mathematically, you’d need an equation that deals with lots of change, like, say, a differential equation. In fact, you might even need a system of differential equations, because you have to keep track of the cat’s shape, position, speed, and probably a few other variables.
Going back to linear algebra for a moment, you can perform some matrix operations on this system of differential equations to produce what are called eigenvectors. It’s not really important what eigenvectors are, except to know that they form the basis for the solution space.
To explain what a basis is, I’m going to steal from Dr. Armstrong for a moment. The example she gave of a genetic algorithm at work was one in which a “population” of cookie recipes are baked, and the more successful recipes pass on their “genes” to the next generation. A gene, in this sense, is the individual components of the recipe: sugar, flour, chocolate chips, etc.
You have some number of cups of sugar, add that onto some number of cups of flour, add that onto some number of cups of chocolate chips, and so on, and you have a cookie recipe. These linear combinations of ingredients—different numbers of cups—can be used to form a vast set of cookie recipes, a solution space of cookie recipes, if you will. So a basis is the core ingredients with which you can build an infinite variety of a particular item.
Let’s get back to our cat example. If you take a system of linear differential equations about falling cats and find their eigenvectors, then you will have a basis for the solution space of cat falling. That is, you will know an infinite number of ways that a cat can fall, given some initial conditions. But what ways of falling are better than others? That’s where genetic algorithms come in.
In our case, a genetic algorithm is what produced the cat righting reflex. You see, as we discovered, there are an infinite number of ways for a cat to fall. (While there are an infinite number of solutions, infinity is not everything. For example, there are an infinite number of numbers between 0 and 1, but the numbers between 0 and 1 are not all the numbers. Similarly, there are ways in which you can arrange the equations of cat falling that don’t produce meaningful results, like a cat falling up, so these aren’t a part of the infinite solution space.)
It would take a very long time to search through an infinite number of cat falling techniques to find the best one. Genetic algorithms, then, take a population of cats, have a lot of them fall, and see which ones fall better than others. This is, of course, natural selection. Now, you may think of evolution as a slow process, but it’s important to remember that this genetic algorithm is not just testing the fitness of cat falling, but of every other way in which a cat could possibly die. From that standpoint, evolution has done an absolutely remarkable job of creating an organism that can survive in a great many situations.
If you don’t believe me, consider that there is a Wikipedia page dedicated to the “falling cat problem” which, among other things, compares the mathematics of falling cats to the mathematics of quantum chromodynamics (which I don’t understand a lick of, btw).
Some of you may be wondering how what is essentially a search algorithm can be considered a form of “artificial intelligence.” Well, to answer that question, you have to give a good definition of what intelligence really is. But this blog post is probably long enough already, so I’m not going down that road. Consider for a moment, however, that there is a certain segment of the population that is absolutely convinced life originated via intelligent design. While their opinion on this matter is almost always bound up in belief, it’s not hard to look at nature and see something intelligent. If nothing else, nature produced humans, and it’s difficult to imagine any definition of intelligence that doesn’t include us (despite our occasional idiocy).
One final note: I lied in the beginning. I think Solution Space would make an excellent title for an SF story, so there’s your connection to science fiction and writing. And don’t steal my title, Mr. Martin.
Tuesday, October 8, 2013
The Wait
Due to fortuitous timing, my life is in somewhat of a holding pattern at the moment. There are three upcoming events that I can do nothing more than wait for. I will list them now in order of my increasing impotence to influence.
A week ago, I submitted a short story to a magazine. They say their average response time is five weeks, which means I have to wait another four weeks until they send me my rejection notice. With any luck, it will be a personal rejection.
This is the first story I’ve submitted for publication in several years. I think it’s probably the best thing I’ve ever written, and I know it’s decent enough to be published, but I shouldn’t fool myself into thinking that the first (or fifth, or tenth) publication I send it to will agree with me.
I was spurred into finally submitting a short story because a very good friend of mine just made her first sale. Unlike me, she’s been submitting non-stop for most of this year. Also unlike me, she’s been sending her stories to the myriad online magazines that have sprung up in recent years. I’ve sent my story, an 8,000-word behemoth, to the magazine for science fiction, because I have delusions of grandeur, apparently.
Moving on to the second item on my list, October is when I am supposed to hear back from the 4-year school I’m hoping to attend this coming spring. Their answer, unlike the magazine I’m submitting to, should be a positive one. Theoretically, I’m enrolled in a transfer program between my community college and the university that guarantees my admission so long as I keep my grades up and yada yada.
I’ve done all that, but I was still required to submit an application along with everyone else that wants to attend the school. And I’ve still been required to wait until now to receive word on my admission. All this waiting has me doubting how guaranteed my admission really is, but I’m still optimistic that the wait amounts to nothing more than a slow-moving bureaucracy. We’ll see.
Additionally, assuming I am admitted to the university, I then have to figure out how I’m paying for my schooling (community college is much cheaper) and how well my community college transcript transfers to my 4-year school. The hassle over figuring out what classes count as what could make for a whole other post. I haven’t decided yet whether I want to bore my three readers with the details.
And finally, as I hinted at in my last post, I’m a government contractor currently experiencing the joys of a government shutdown. So I’m waiting for our duly elected leaders to do their jobs and let me do my job. This is decidedly not a political blog, and I don’t want to get mired in partisan debates, but I have to say that I would much rather a system that doesn’t grind to a halt whenever opposing sides fail to reach an agreement.
There are a lot of theoretical alternatives to the system of representative democracy that we have, but I honestly don’t know enough about the subject to know which one would be better. Each system has pros and cons, and it is my limited understanding that no form of democracy is capable of perfectly representing the will of the people. If that’s the case, what hope is there for the future of civilization? Well, we can hope for an increasingly less imperfect future, I suppose. Or, to return to the SF side of things, we could just ask Hari Seldon to plan out the future for us.
The one political statement I’ll make here is that I never got over the wonder of Asimov’s psychohistory. I am a firm proponent of technocracy and the idea that, sometimes, it’s better to let experts make decisions about complex topics. Where I think democracy has its place is in ensuring that people are allowed to choose the type of society they want to live in. But if they really do want to live in society X, then they should let capable experts create society X first.
Okay, I think that’s enough pontificating for now. Is there some deeper connection between the three things I’m waiting for? Some thread that ties it all together? A concept from physics or mathematics that I can clumsily wield as an analogy? Nope. Sorry. Not this time.
A week ago, I submitted a short story to a magazine. They say their average response time is five weeks, which means I have to wait another four weeks until they send me my rejection notice. With any luck, it will be a personal rejection.
This is the first story I’ve submitted for publication in several years. I think it’s probably the best thing I’ve ever written, and I know it’s decent enough to be published, but I shouldn’t fool myself into thinking that the first (or fifth, or tenth) publication I send it to will agree with me.
I was spurred into finally submitting a short story because a very good friend of mine just made her first sale. Unlike me, she’s been submitting non-stop for most of this year. Also unlike me, she’s been sending her stories to the myriad online magazines that have sprung up in recent years. I’ve sent my story, an 8,000-word behemoth, to the magazine for science fiction, because I have delusions of grandeur, apparently.
Moving on to the second item on my list, October is when I am supposed to hear back from the 4-year school I’m hoping to attend this coming spring. Their answer, unlike the magazine I’m submitting to, should be a positive one. Theoretically, I’m enrolled in a transfer program between my community college and the university that guarantees my admission so long as I keep my grades up and yada yada.
I’ve done all that, but I was still required to submit an application along with everyone else that wants to attend the school. And I’ve still been required to wait until now to receive word on my admission. All this waiting has me doubting how guaranteed my admission really is, but I’m still optimistic that the wait amounts to nothing more than a slow-moving bureaucracy. We’ll see.
Additionally, assuming I am admitted to the university, I then have to figure out how I’m paying for my schooling (community college is much cheaper) and how well my community college transcript transfers to my 4-year school. The hassle over figuring out what classes count as what could make for a whole other post. I haven’t decided yet whether I want to bore my three readers with the details.
And finally, as I hinted at in my last post, I’m a government contractor currently experiencing the joys of a government shutdown. So I’m waiting for our duly elected leaders to do their jobs and let me do my job. This is decidedly not a political blog, and I don’t want to get mired in partisan debates, but I have to say that I would much rather a system that doesn’t grind to a halt whenever opposing sides fail to reach an agreement.
There are a lot of theoretical alternatives to the system of representative democracy that we have, but I honestly don’t know enough about the subject to know which one would be better. Each system has pros and cons, and it is my limited understanding that no form of democracy is capable of perfectly representing the will of the people. If that’s the case, what hope is there for the future of civilization? Well, we can hope for an increasingly less imperfect future, I suppose. Or, to return to the SF side of things, we could just ask Hari Seldon to plan out the future for us.
The one political statement I’ll make here is that I never got over the wonder of Asimov’s psychohistory. I am a firm proponent of technocracy and the idea that, sometimes, it’s better to let experts make decisions about complex topics. Where I think democracy has its place is in ensuring that people are allowed to choose the type of society they want to live in. But if they really do want to live in society X, then they should let capable experts create society X first.
Okay, I think that’s enough pontificating for now. Is there some deeper connection between the three things I’m waiting for? Some thread that ties it all together? A concept from physics or mathematics that I can clumsily wield as an analogy? Nope. Sorry. Not this time.
Monday, September 30, 2013
On the Merits of Underwater Basket Weaving
I remember thinking awhile back that I wanted to post once a week. Well, here’s me trying for once a month. I really do intend to post more frequently, and if a certain political event comes to pass I just might have quite a bit of free time. We’ll see.
Anywho, today we’re going to talk about underwater basket weaving and its part in the End Times. There’s been a great deal of hubbub recently about education, about how it’s too expensive, or how our students are getting dumber by the minute, or how our universities are liberal brainwashing factories. You’ve heard it all. These are complex subjects without easy answers (which is kind of the point of this post), and I won’t presume to know what to do about them.
But there’s another talking point I’ve heard recently that I’d like to delve into a bit more deeply. You see, some people are taking the wrong classes. Not only that, but some people are majoring in the wrong subjects! Yes, that’s right, some people go to school for English, art history, philosophy, gender studies, or worse. What makes these the wrong subjects? Well, I’m a STEM major, and those are not STEM subjects, so clearly they are incorrect.
Wait, no, I’m sure there has to be more to it than that. Oh yes, it’s about money. Those other majors, you know, are a bit lacking in the career prospects department. You can’t major in underwater basket weaving and expect to have a six-figure underwater basket weaving job waiting for you on the other side of your diploma. Which is all well and good and none of my concern except that you’ve probably got five-figure student loans from the government that you’re not paying off, so you’re nothing but a parasitic leach on the meaty thighs of America.
And that brings us to the McNamara fallacy. This fallacy is best summed up in a quote about it from some guy named Daniel Yankelovich:
Historically, it was far easier to measure the sun’s apparent motion around the Earth than to measure the changing phases of Venus. The result: people believed the Earth was the center of the universe.
Historically, it was far easier to measure an object’s apparently natural deceleration than to measure the effects of friction. The result: people erroneously believed Aristotelian physics until Galileo and Newton came along.
There are plenty of other examples throughout history where insufficient means of observation led to incorrect conclusions. We cannot fault our ancestors for not having the tools we have, but we can fault ourselves for not heeding this lesson.
What am I getting at here? Well, it’s relatively easy to measure the economic potential of a particular educational choice. We can say with a fair degree of certainty that a mechanical engineer or computer scientist is very often going to make a good deal more money than a historian or poet. And by making more money, said individual will be a positive return on the investment that is the college loan.
Is that important? Probably. Wealthier nations tend to have greater scientific progress, less poverty, more freedom, etc. There are definitely some strong correlations between wealth and general awesomeness. But if all we measure is economic output, then we’re falling prey to the McNamara fallacy. What other measurements could we be performing?
I’m clearly not the only person to question the singular importance of STEM. Proponents of the humanities and liberal arts have written a great deal about the value of a less mathy education. A liberal arts education teaches you to be a better citizen, to be moral, to ask big questions, etc. And that all sounds good, but to a STEM major like me, it also sounds thoroughly unquantifiable.
There are two issues here. The first is that there may be hard to measure variables more strongly correlated with being awesome than economic output is. The second is that our definition of awesome may be based on our measure of economic productivity, leading us to miss other ways of being.
If the former is true, then we need to figure out ways to measure the value of an education in the humanities. Rather than simply studying philosophy or literature or art, we need to study the effects these subjects have on the brain, both neurologically and psychologically. One of the mantras of the humanities is that truth is discovered within the human mind. Well, I don’t presume to know what truth is, but I do know that science has made more discoveries than any other human endeavor ever has, so perhaps it can find the mind’s hidden truths.
If the latter case is true, and what we think of as the good life and success are not the end all be all (this and the former issue are not mutually exclusive, by the way), then it’s a bit harder to say what comes next. I have my own ideas, personally. I have an entire philosophical framework that underlies what I believe is important and meaningful, but there’s no particular reason why anyone should subscribe to my crazy ideas.
I can say this, however. We’ve been doing roughly the same thing for several thousand years now. Your average schmuck struggles to get by, to raise a family and live a fulfilling life, while toiling away at whatever job is required. But maybe that’s not the only way things can be. How else might we live a life? Well, let’s figure that out. Let's experiment and gather data. Instead of just studying philosophy, instead of reading about it in books and discussing what others have said, let’s do philosophy. Let’s make understanding life, morality, and knowledge central parts of being a citizen, and then we can see what sort of lives we end up living.
Anywho, today we’re going to talk about underwater basket weaving and its part in the End Times. There’s been a great deal of hubbub recently about education, about how it’s too expensive, or how our students are getting dumber by the minute, or how our universities are liberal brainwashing factories. You’ve heard it all. These are complex subjects without easy answers (which is kind of the point of this post), and I won’t presume to know what to do about them.
But there’s another talking point I’ve heard recently that I’d like to delve into a bit more deeply. You see, some people are taking the wrong classes. Not only that, but some people are majoring in the wrong subjects! Yes, that’s right, some people go to school for English, art history, philosophy, gender studies, or worse. What makes these the wrong subjects? Well, I’m a STEM major, and those are not STEM subjects, so clearly they are incorrect.
Wait, no, I’m sure there has to be more to it than that. Oh yes, it’s about money. Those other majors, you know, are a bit lacking in the career prospects department. You can’t major in underwater basket weaving and expect to have a six-figure underwater basket weaving job waiting for you on the other side of your diploma. Which is all well and good and none of my concern except that you’ve probably got five-figure student loans from the government that you’re not paying off, so you’re nothing but a parasitic leach on the meaty thighs of America.
And that brings us to the McNamara fallacy. This fallacy is best summed up in a quote about it from some guy named Daniel Yankelovich:
The first step is to measure whatever can be easily measured. This is OK as far as it goes. The second step is to disregard that which can't be easily measured or to give it an arbitrary quantitative value. This is artificial and misleading. The third step is to presume that what can't be measured easily really isn't important. This is blindness. The fourth step is to say that what can't be easily measured really doesn't exist. This is suicide.Now, you can look on Wikipedia, see that this is poorly sourced, wonder whether it’s really a fallacy, and point out that this fallacy is used by purveyors of pseudoscience to avoid having to prove their claims, but I want you to stick with me anyway. The gist of the argument is that it’s unwise to believe that easily measured variables are more important than not so easily measured variables. Historically, this is definitively true.
Historically, it was far easier to measure the sun’s apparent motion around the Earth than to measure the changing phases of Venus. The result: people believed the Earth was the center of the universe.
Historically, it was far easier to measure an object’s apparently natural deceleration than to measure the effects of friction. The result: people erroneously believed Aristotelian physics until Galileo and Newton came along.
There are plenty of other examples throughout history where insufficient means of observation led to incorrect conclusions. We cannot fault our ancestors for not having the tools we have, but we can fault ourselves for not heeding this lesson.
What am I getting at here? Well, it’s relatively easy to measure the economic potential of a particular educational choice. We can say with a fair degree of certainty that a mechanical engineer or computer scientist is very often going to make a good deal more money than a historian or poet. And by making more money, said individual will be a positive return on the investment that is the college loan.
Is that important? Probably. Wealthier nations tend to have greater scientific progress, less poverty, more freedom, etc. There are definitely some strong correlations between wealth and general awesomeness. But if all we measure is economic output, then we’re falling prey to the McNamara fallacy. What other measurements could we be performing?
I’m clearly not the only person to question the singular importance of STEM. Proponents of the humanities and liberal arts have written a great deal about the value of a less mathy education. A liberal arts education teaches you to be a better citizen, to be moral, to ask big questions, etc. And that all sounds good, but to a STEM major like me, it also sounds thoroughly unquantifiable.
There are two issues here. The first is that there may be hard to measure variables more strongly correlated with being awesome than economic output is. The second is that our definition of awesome may be based on our measure of economic productivity, leading us to miss other ways of being.
If the former is true, then we need to figure out ways to measure the value of an education in the humanities. Rather than simply studying philosophy or literature or art, we need to study the effects these subjects have on the brain, both neurologically and psychologically. One of the mantras of the humanities is that truth is discovered within the human mind. Well, I don’t presume to know what truth is, but I do know that science has made more discoveries than any other human endeavor ever has, so perhaps it can find the mind’s hidden truths.
If the latter case is true, and what we think of as the good life and success are not the end all be all (this and the former issue are not mutually exclusive, by the way), then it’s a bit harder to say what comes next. I have my own ideas, personally. I have an entire philosophical framework that underlies what I believe is important and meaningful, but there’s no particular reason why anyone should subscribe to my crazy ideas.
I can say this, however. We’ve been doing roughly the same thing for several thousand years now. Your average schmuck struggles to get by, to raise a family and live a fulfilling life, while toiling away at whatever job is required. But maybe that’s not the only way things can be. How else might we live a life? Well, let’s figure that out. Let's experiment and gather data. Instead of just studying philosophy, instead of reading about it in books and discussing what others have said, let’s do philosophy. Let’s make understanding life, morality, and knowledge central parts of being a citizen, and then we can see what sort of lives we end up living.
Tuesday, August 13, 2013
On the Particular Qualities of Good SF
I’m a little late on the review bandwagon, but this post is
more or less inspired by my thoughts on star:
trek Into darkness. If you haven’t seen the movie yet, you should cover
your eyes while you read this part because here’s the spoiler to the
earth-shattering final twist of the movie: Kirk doesn’t die. I know, I know—shocking.
How the writers managed to keep a lid on that one is anyone’s guess.
Anyway, why doesn’t Kirk die? It turns out the reason he
doesn’t die is because the brilliant physician Bones McCoy has made a
monumental discovery in medicine that will change every life in the Federation
forever and surely be the focal point of the next Star Trek movie. Yes, Bones
has managed to discover the secret to immortality in the blood of a man created
with 200 year old technology.
At least one thing I said in the preceding paragraph is
true. (There will be another Star Trek movie.) But let’s put aside the snark
for a moment. Why does this grate me so? Because it’s a missed opportunity. If
Bones really had discovered immortality, and it really did change the
Federation in some way, then that would make for some pretty interesting
science fiction. Instead it will likely never be mentioned again, because it
was only a gimmick to create suspense at the end of the movie.
But who cares about discussing immortality, right? It’s
never going to happen, or life is only meaningful because of death, or it’s
just some nerd boy’s fantasy, right? Well, yes, immortality isn’t real, but
that would seem to make it excellent fodder for fiction. Good fiction is
traditionally supposed to explore the human condition, and that’s a nearly
endless fount from which to plumb. There’s love, hatred, war, jealousy, and all
that other good human condition stuff. But those elements of the human
condition are the low-hanging fruit; they’ve been picked. What else is being human about?
If there are examples we can point to that are solidly
within the domain of the human condition, then the next place we can look is
outward at the edge cases. Edge is a good word here. After all, how do you identify
objects you can see? You look to the edge of the thing, see where it stops, trace
its shape. If you want to know what something is, find out where it stops and
draw a line.
I’m reminded of a topic from linear algebra that might make
for a useful analogy or might just confuse people even more. Stick with me.
Take a matrix with, say, 10 columns. If this matrix is full of unknowns, then
there’s a method for figuring out every single way to add those unknowns
together and come out with 0.
This is called the nullspace of a matrix. In essence, it
tells you everything a matrix is not. The nullspace of a matrix is described by
a number of dimensions. Let’s say we have a matrix with a nullspace of 6
dimensions. One of the neat things about linear algebra is that the number of
columns (10) minus the dimensions of the nullspace (6) is always equal to the dimensions of the
row space (4). What’s the row space? Well, in short, it’s everything a matrix could
be. What does that all mean? It means that you can find out what something is by figuring out what it’s not.
Which takes us back to science fiction. Good science fiction
tells us about the human condition specifically by telling us about something
other than the human condition. It tells us about things near the human
condition, at the edge, making up the border. And by doing so, it lets us
create a rough outline of what the human condition really looks like.
So, then, magic is science fiction, right? I mean, it’s definitely
not human, which means stories about it tell us about what is human, right? Ah,
uh, no. The key here is that you have to look at the edges of a thing where you
think it might be. The reason is that there’s generally a lot more that a thing
isn’t than a thing is.
If you’ll allow me, let’s return to the linear algebra
example. If the nullspace of a matrix is infinite and the row space is finite,
then I can start calling out random numbers and have a pretty good chance of giving
you a number in the nullspace rather than the row space. But what does this
tell me about the matrix? Basically nothing. However, when you’re done finding
the nullspace of a matrix, you’re left with a formula that tells you how to figure
out what’s in it. The formula lets you extract useful information from the
problem.
A formula is basically just a set of rules to follow. And it’s
these rules that get to the heart of good science fiction. They let you find the
line between what’s human and what’s not. Technology in fiction might follow
rules, but it also might not. That’s the difference between your hard SF and
something like Star Wars. Star Wars has lasers and spaceships, but they don’t
follow any rules, which means they’re not telling you anything about the boundaries
of the human condition.
And it’s also the difference between good science fiction
and the most recent Star Trek movie. Because we’re never going to see Khan’s
immortal blood again, it’s not following any rules; it’s essentially magic. If
it had been explored as a topic, we could have learned something from it.
Now, magic systems in high fantasy might have intricate
rules, but if those rules are describing something completely alien, they’re not
telling you about what it means to be or not be human. In linear algebra, it’s
akin to knowing the formula for a different matrix. It tells you something, but
it doesn’t tell you what you want to know.
By the way, I’m not bashing Star Wars or fantasy. Both of
them can be good fiction, and both of them can tell you things about the human
condition. But they’re really only doing so the old-fashioned way—by looking at
what we know for certain is human. They’re not doing it by exploring the edge
cases.
But we need to explore the edge cases; we need to find the
rules. Why? Because eventually we’re going to pick all the low-hanging fruit
and we’re not going to have anything new to say about the human condition. The
only way we’ll be able to keep learning about ourselves is by finding our
boundaries and pressing up against them. And the best way to do that is by
writing good science fiction.
Friday, August 2, 2013
This Is What You’re Really Doing
Again, it’s been awhile since my last post. Stuffing linear algebra into a 5-week course (with a not terribly awesome professor) turned out to be hard. But I said I would have a post about the class, and last night presented the nth example of what it is I wanted to write about.
You see, linear algebra is no ordinary math class, despite the deceptively benign name. Our professor told us we’d actually have to think in his class because linear algebra is the first math course where you have to prove things. That’s true enough, but it’s not the reason why linear algebra is different from other math.
The reason is that linear algebra is the first math course seemingly dedicated to the task of teaching you what you’re really doing in math. We kind of take it for granted that our teachers lie to us. They don’t (usually) do so maliciously; they do so because the “true” answer is significantly more complex than the “false” answer. But it happens pretty frequently that the lies teachers tell us are good enough.
Regardless, there comes a point at which you’re deemed capable of handling the truth. Now, there are plenty of times earlier in math when this happens. I think the most basic example is subtraction. You learn it shortly after you learn about addition, and you’re told that unlike addition, subtraction is not commutative. 10-5 is not the same as 5-10. But it turns out that whenever you’re subtracting, what you’re “really” doing is adding a negative. 10-5 becomes 10 + -5. And then subtraction is again commutative, because 10 + -5 is exactly the same as -5 + 10.
But linear algebra extends this drawing back of the curtain to many more ideas. In linear algebra, you learn that the vector dot product is really just a special case of a general operation called the inner product. You learn that vectors themselves are really just objects that follow a particular set of rules and don’t necessarily have anything to do with directed line segments. You learn that functions are really just a method of mapping one set to another.
At this point you might be wondering what “really” really means. Is there some true math underlying the universe that we simple humans are merely discovering, or are we just peeling back the layers of logic upon which our peculiar brand of mathematics is built? Since the 1600s, when calculus was discovered/invented, mathematics has proven enormously successful at describing the real world.
Many have seen this as distinct evidence that math is something real and not just a human construct. Math that was once thought to be purely theoretical in nature has turned out to have physical basis. So when a mathematician writes down a law no one has written down before, has that mathematician discovered the law or invented it?
Others do not hold math in such reverence, choosing to believe instead that we have simply made up math to serve our purposes. They point to the fact that mathematicians often make choices and that those choices don’t necessarily reflect anything deeper. We choose for 0! to equal 1. We choose for division by zero to give you a calculator error. At one point we chose for there to be no imaginary numbers or even negative ones. Did someone discover the complex numbers, or did we merely decide to define the square root of -1?
I try not to make definitive statements about the nature of the universe. I err on the side of caution as far as that’s concerned. So I’m not willing to say that math is a fundamental part of the universe. But I also don’t believe new branches of math are merely choices or inventions. Instead I believe that new math resembles the emergent phenomena you see in something like the Game of Life. Simple rules can lead to complex behavior. DNA is truly the perfect example. There is far more data contained in even an infant human brain than in the human genome, yet somehow the brain comes from DNA, from following relatively simple rules over and over again.
Math, then, is many complex rules that emerge from a few simple ones. Historically, mathematics began by matching sets. We used numbers to keep track of livestock in a pen or bushels of grain in a granary. We matched the number we observed with the number of notches in clay or wood. And it turns out that today—although this wasn’t always true—we still base mathematics on the idea of matching and counting sets.
So when a mathematician writes down a new law, that mathematician is discovering a novel application of the rules we invented. This doesn’t explain why math is so effective, but it does bridge a gap between discovery and invention.
The next question, I suppose, is why we invented the rules we did. I think that arises from the fact that, on large-ish scales, the universe is discrete. I see 1 tasty lamb; I’m being chased by 3 hungry wolves; I am saved by 5 human friends.
(On small-ish scales, the universe looks continuous. We don’t have 3 water; we have enough water to fill that bucket. We now know that water is made up of molecules, so you can count your water.)
Maybe that’s why it took us so long to get to calculus. Maybe our brains are designed to see things in a discrete, delineated fashion. We know it’s true that our brains are excellent at border detection, at filling in missing lines, at assigning meaning to individual objects. So perhaps our universe exists discretely, and we evolved discretely, and we came up with discrete math, too. No wonder the math we invented, and then discovered, is so effective.
(No, I don't believe I've solved the philosophy of mathematics in a 1000-word post.)
You see, linear algebra is no ordinary math class, despite the deceptively benign name. Our professor told us we’d actually have to think in his class because linear algebra is the first math course where you have to prove things. That’s true enough, but it’s not the reason why linear algebra is different from other math.
The reason is that linear algebra is the first math course seemingly dedicated to the task of teaching you what you’re really doing in math. We kind of take it for granted that our teachers lie to us. They don’t (usually) do so maliciously; they do so because the “true” answer is significantly more complex than the “false” answer. But it happens pretty frequently that the lies teachers tell us are good enough.
Regardless, there comes a point at which you’re deemed capable of handling the truth. Now, there are plenty of times earlier in math when this happens. I think the most basic example is subtraction. You learn it shortly after you learn about addition, and you’re told that unlike addition, subtraction is not commutative. 10-5 is not the same as 5-10. But it turns out that whenever you’re subtracting, what you’re “really” doing is adding a negative. 10-5 becomes 10 + -5. And then subtraction is again commutative, because 10 + -5 is exactly the same as -5 + 10.
But linear algebra extends this drawing back of the curtain to many more ideas. In linear algebra, you learn that the vector dot product is really just a special case of a general operation called the inner product. You learn that vectors themselves are really just objects that follow a particular set of rules and don’t necessarily have anything to do with directed line segments. You learn that functions are really just a method of mapping one set to another.
At this point you might be wondering what “really” really means. Is there some true math underlying the universe that we simple humans are merely discovering, or are we just peeling back the layers of logic upon which our peculiar brand of mathematics is built? Since the 1600s, when calculus was discovered/invented, mathematics has proven enormously successful at describing the real world.
Many have seen this as distinct evidence that math is something real and not just a human construct. Math that was once thought to be purely theoretical in nature has turned out to have physical basis. So when a mathematician writes down a law no one has written down before, has that mathematician discovered the law or invented it?
Others do not hold math in such reverence, choosing to believe instead that we have simply made up math to serve our purposes. They point to the fact that mathematicians often make choices and that those choices don’t necessarily reflect anything deeper. We choose for 0! to equal 1. We choose for division by zero to give you a calculator error. At one point we chose for there to be no imaginary numbers or even negative ones. Did someone discover the complex numbers, or did we merely decide to define the square root of -1?
I try not to make definitive statements about the nature of the universe. I err on the side of caution as far as that’s concerned. So I’m not willing to say that math is a fundamental part of the universe. But I also don’t believe new branches of math are merely choices or inventions. Instead I believe that new math resembles the emergent phenomena you see in something like the Game of Life. Simple rules can lead to complex behavior. DNA is truly the perfect example. There is far more data contained in even an infant human brain than in the human genome, yet somehow the brain comes from DNA, from following relatively simple rules over and over again.
Math, then, is many complex rules that emerge from a few simple ones. Historically, mathematics began by matching sets. We used numbers to keep track of livestock in a pen or bushels of grain in a granary. We matched the number we observed with the number of notches in clay or wood. And it turns out that today—although this wasn’t always true—we still base mathematics on the idea of matching and counting sets.
So when a mathematician writes down a new law, that mathematician is discovering a novel application of the rules we invented. This doesn’t explain why math is so effective, but it does bridge a gap between discovery and invention.
The next question, I suppose, is why we invented the rules we did. I think that arises from the fact that, on large-ish scales, the universe is discrete. I see 1 tasty lamb; I’m being chased by 3 hungry wolves; I am saved by 5 human friends.
(On small-ish scales, the universe looks continuous. We don’t have 3 water; we have enough water to fill that bucket. We now know that water is made up of molecules, so you can count your water.)
Maybe that’s why it took us so long to get to calculus. Maybe our brains are designed to see things in a discrete, delineated fashion. We know it’s true that our brains are excellent at border detection, at filling in missing lines, at assigning meaning to individual objects. So perhaps our universe exists discretely, and we evolved discretely, and we came up with discrete math, too. No wonder the math we invented, and then discovered, is so effective.
(No, I don't believe I've solved the philosophy of mathematics in a 1000-word post.)
Thursday, July 11, 2013
I Don’t Know Anything About Economics
Sorry for the
long gap between posts. A lot’s been going on recently. Anywho, I’ve
started up my linear algebra class, so hopefully I’ll have some
interesting things to post about that soon. I’ve already learned
techniques that would have made problems in both E&M and multivariable calculus a lot easier to solve. Oh, well.
But on to the meat of this post. Re: economics, it’s not strictly speaking true that I know nothing about it. Like most sciences, I’ve paid enough attention to get a general idea of what it’s about. I even took a semester of economics in high school, but it was taught by a brand new teacher who used to be a banker and for some reason felt the need to confide in us that he didn’t actually have a teaching certificate and we really shouldn’t tell anyone that. Oops.
On the whole, however, my knowledge of the dismal science is quite limited. But economics is a science, however sad and soft it may be. And I think this is an important fact that a lot of people seem to forget, which is where this post is coming from.
You see, I used to have very strong opinions about economics. (Those that know me in real life may wonder about the “used to” there, but I think it’s largely true.) I was raised in a leftish household and with that came mostly leftish politics and economics. My politics, however, took a turn toward the weird after a bit of philosophical revelation ten years ago. But my economics remained mostly leftish for a long time.
Recently, however, that’s begun to change. Now, this isn’t the story of me transforming into a commie-hating libertarian, or even someone who’s moderately right, or even someone who is staunchly in the middle. Rather, this is the story of me deciding that if I don’t actually know anything about economics, I shouldn’t have (strong) opinions about it.
As I said, economics is a science. And in science, there are two kinds of debates you can have: debates where the answer is already known but one side refuses to acknowledge it, and debates where an answer won’t be forthcoming until more data is collected.
For example, there is a “debate” about whether evolution is true. As far as science is concerned, this debate is quite settled and has been for a long time (up to a hundred and fifty years). Some believe the issue is not settled, but their belief is incorrect. That’s not to say their beliefs in general are wrong—just their beliefs about evolution.
And then there’s the second kind of debate, where we just don’t know enough yet. Take cosmology’s dark energy as an example. Dark energy is a proposed mechanism to explain the observed accelerating expansion of the universe, but cosmologists don’t yet know what dark energy really is. There are theories, but no solid evidence. A good cosmologist may prefer one theory over another, and argue its case, but a good cosmologist will also ultimately admit ignorance on the topic. More data is needed before the issue can be settled.
In both of these scenarios, the right answer is not decided upon by the voting public. In the case of evolution, a vote is inappropriate because one answer is obviously correct and the public may vote incorrectly. In the case of dark energy, it’s too early to hold a vote because the answer isn’t known yet. But in both cases, there’s not ever a situation in which the public should be voting on the issue because the public is not informed enough about the topic to make the correct choice (except by accident).
You see where I’m going with this. If economics is a real science that requires years of study to master, then economic questions are either settled (and should simply be policy) or not settled (and should be left to experts to study). Thus, when I vote, I don’t really do it based on economic policy. Philosophically speaking, there are issues that are more important to me, and about which I am more knowledgeable.
Some may see this as cowardice. I’m too wishy-washy to take a stance, too scared of being wrong. But I (surprise!) see it differently. I think one of the most important lessons of science is that it’s okay to say you don’t know, okay to profess ignorance. In the words of Newton, “Hypotheses non fingo.” You don’t have to invent explanations when you can’t see one. You don’t have to come to a conclusion before you have all the data.
In fact, I think admitting ignorance can be seen as a brave act. Belief is hard-wired in humans; it’s what we do naturally. We observe a phenomenon and we attribute a cause to it, no matter how tenuous the connection, because we’re scared of not knowing. Withholding judgment, however, is much harder, and takes care and concentration.
Some may see my lack of an opinion as irresponsible. While many sciences tend toward the academic and lack real-world consequences, economics is, by definition, something we cannot ignore. Resources are scarce and we have to do something about it. By refraining from taking a stance on economic issues, I refrain from solving the problem of allocating scarce resources.
But I think that perspective misses the point, which is that resources are scarce and that’s not going to change any time soon. There’s no solution within economics to the fact of scarcity, only solutions to dealing with it. As far as I’m concerned, the best solution is to eliminate the need for economics completely. With sufficiently advanced technology, we can have practically unlimited resources. We’re nowhere close to that, and in the long run it’s distinctly untrue, but it can be true within the lifetime of our species.
Again, we’ve stumbled on another reason why I’ve decided to study science. It may seem as if I’m a delusional believer in a techno-utopia… and I’m not going to deny that. Getting into why that’s the case would require another post, however, and I think this one is long enough as it is.
So in the meantime I think it’s best to leave economics to the economists and be okay with admitting ignorance.
But on to the meat of this post. Re: economics, it’s not strictly speaking true that I know nothing about it. Like most sciences, I’ve paid enough attention to get a general idea of what it’s about. I even took a semester of economics in high school, but it was taught by a brand new teacher who used to be a banker and for some reason felt the need to confide in us that he didn’t actually have a teaching certificate and we really shouldn’t tell anyone that. Oops.
On the whole, however, my knowledge of the dismal science is quite limited. But economics is a science, however sad and soft it may be. And I think this is an important fact that a lot of people seem to forget, which is where this post is coming from.
You see, I used to have very strong opinions about economics. (Those that know me in real life may wonder about the “used to” there, but I think it’s largely true.) I was raised in a leftish household and with that came mostly leftish politics and economics. My politics, however, took a turn toward the weird after a bit of philosophical revelation ten years ago. But my economics remained mostly leftish for a long time.
Recently, however, that’s begun to change. Now, this isn’t the story of me transforming into a commie-hating libertarian, or even someone who’s moderately right, or even someone who is staunchly in the middle. Rather, this is the story of me deciding that if I don’t actually know anything about economics, I shouldn’t have (strong) opinions about it.
As I said, economics is a science. And in science, there are two kinds of debates you can have: debates where the answer is already known but one side refuses to acknowledge it, and debates where an answer won’t be forthcoming until more data is collected.
For example, there is a “debate” about whether evolution is true. As far as science is concerned, this debate is quite settled and has been for a long time (up to a hundred and fifty years). Some believe the issue is not settled, but their belief is incorrect. That’s not to say their beliefs in general are wrong—just their beliefs about evolution.
And then there’s the second kind of debate, where we just don’t know enough yet. Take cosmology’s dark energy as an example. Dark energy is a proposed mechanism to explain the observed accelerating expansion of the universe, but cosmologists don’t yet know what dark energy really is. There are theories, but no solid evidence. A good cosmologist may prefer one theory over another, and argue its case, but a good cosmologist will also ultimately admit ignorance on the topic. More data is needed before the issue can be settled.
In both of these scenarios, the right answer is not decided upon by the voting public. In the case of evolution, a vote is inappropriate because one answer is obviously correct and the public may vote incorrectly. In the case of dark energy, it’s too early to hold a vote because the answer isn’t known yet. But in both cases, there’s not ever a situation in which the public should be voting on the issue because the public is not informed enough about the topic to make the correct choice (except by accident).
You see where I’m going with this. If economics is a real science that requires years of study to master, then economic questions are either settled (and should simply be policy) or not settled (and should be left to experts to study). Thus, when I vote, I don’t really do it based on economic policy. Philosophically speaking, there are issues that are more important to me, and about which I am more knowledgeable.
Some may see this as cowardice. I’m too wishy-washy to take a stance, too scared of being wrong. But I (surprise!) see it differently. I think one of the most important lessons of science is that it’s okay to say you don’t know, okay to profess ignorance. In the words of Newton, “Hypotheses non fingo.” You don’t have to invent explanations when you can’t see one. You don’t have to come to a conclusion before you have all the data.
In fact, I think admitting ignorance can be seen as a brave act. Belief is hard-wired in humans; it’s what we do naturally. We observe a phenomenon and we attribute a cause to it, no matter how tenuous the connection, because we’re scared of not knowing. Withholding judgment, however, is much harder, and takes care and concentration.
Some may see my lack of an opinion as irresponsible. While many sciences tend toward the academic and lack real-world consequences, economics is, by definition, something we cannot ignore. Resources are scarce and we have to do something about it. By refraining from taking a stance on economic issues, I refrain from solving the problem of allocating scarce resources.
But I think that perspective misses the point, which is that resources are scarce and that’s not going to change any time soon. There’s no solution within economics to the fact of scarcity, only solutions to dealing with it. As far as I’m concerned, the best solution is to eliminate the need for economics completely. With sufficiently advanced technology, we can have practically unlimited resources. We’re nowhere close to that, and in the long run it’s distinctly untrue, but it can be true within the lifetime of our species.
Again, we’ve stumbled on another reason why I’ve decided to study science. It may seem as if I’m a delusional believer in a techno-utopia… and I’m not going to deny that. Getting into why that’s the case would require another post, however, and I think this one is long enough as it is.
So in the meantime I think it’s best to leave economics to the economists and be okay with admitting ignorance.
Subscribe to:
Posts (Atom)